一、實驗目的
1．測定如圖5-2所示試件，沿A-A加載時，即偏心拉伸時的拉應力和彎曲應力。
2．測定如圖5-2所示試件，沿A-A加載時，即偏心拉伸截面中性軸位置。
3．與理論值進行比較分析。
二、實驗儀器和設備
1．拉壓實驗裝置一臺。
2．靜態數字電阻應變儀一臺。
3．偏心拉伸試件一根（已粘貼好應變片）。
三、實驗原理及步驟
1. 實驗原理
拉壓實驗裝置見圖5-1，試件（見圖5-2）就被安裝在上、下夾具中間進行加載。
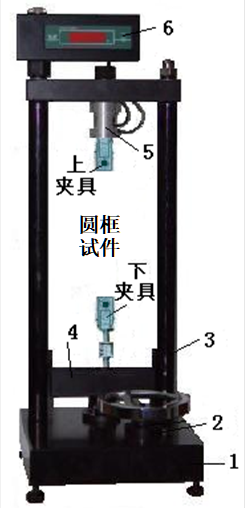
圖5-1 拉壓裝置圖
當載荷加載在試件的對稱軸上，試件的橫截面上只受到軸力，因此又有拉伸正應力。同樣，當載荷加載到了試件的A-A截面上時，此時由拉力引起的正應力和軸對稱加載時產生的拉應力是一樣的，應力為：
（5-1）
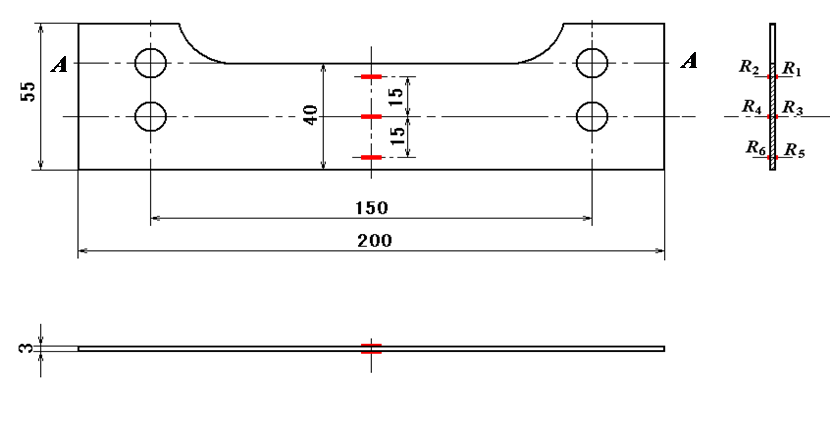
圖5-2 試件貼片圖
但是，當載荷加載到了試件的A-A截面時，試件橫截面上由此產生的正應力分為兩部分，其一是拉力F引起的拉伸應力
，另一部分是彎曲引起的正應力
。因此當載荷加載在A-A截面上時，試件橫截面上的正應力為：
（5-2） 其中，F表示軸力，S表示橫截面面積，M=0.22F表示橫截面上的彎矩，
為形心軸慣性矩，y為距離中性軸的距離（見圖5-3）
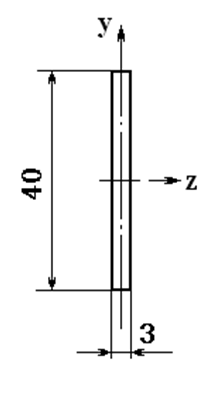
圖5-3 試件橫截面圖
偏心拉伸試件材料彈性模量為70GN/m2。
試件上的貼片情況（見圖5-4），其中對應正反面的應變片已兩兩串聯連接。另有一補償塊，補償塊上共粘貼了四片應變片，其中綠色線為兩片應變片串聯連接線。
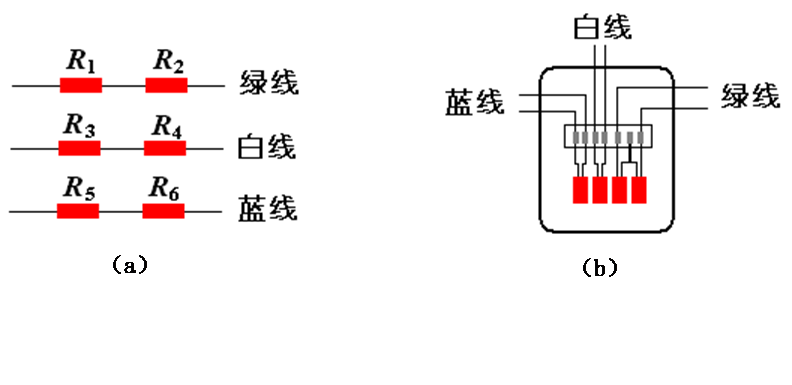
圖5-4 應變片接線圖
2. 實驗步驟
1. 將試件按照軸對稱施加荷載的方式加到裝置上。
2. 打開測力儀開關，將應變片如圖5-5串聯單臂半橋接線法接至應變儀各通道上。
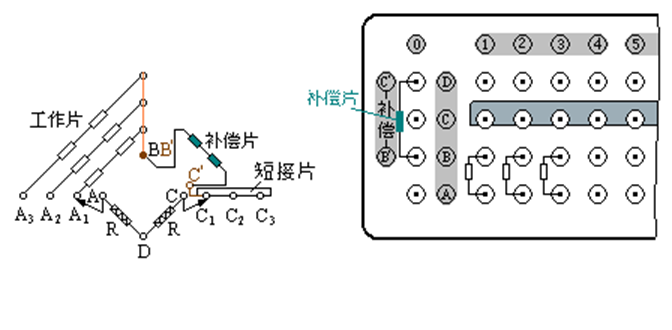
圖5-5 串聯單臂半橋接線法圖
3. 檢查應變儀靈敏系數與應變片是否相同，不同則設置成相同。
4. 進行實驗：
a.加初始載荷0.3kN，將應變儀各通道置零。
b.加至1.3kN，記錄讀數。
c.退回至0.3kN,重新置零。
d.再加載至1.3kN，記錄讀數。如此步驟，重復三次。
5. 換到A-A位置加載，重復步驟4。
四、實驗數據
表5-1 應變記錄表
|
讀數應變 載荷（F）KN |
R1與R2 | R3與R4 | R5與R6 | ||||||||||||
| 1 | 2 | 3 | 平均 | 1 | 2 | 3 | 平均 | 1 | 2 | 3 | 平均 | 1 | 2 | 3 | 平均 |
| 通過對稱軸線加載 | ε1（με） | ε2（με） | ε3（με） | ||||||||||||
| 0.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.3 | 119 | 118 | 119 | 118.7 | 116 | 115 | 115 | 115.3 | 115 | 113 | 114 | 114 | |||
| 0.3 | 2 | 0 | 0 | 0.7 | 1 | 0 | -1 | 0 | 2 | 0 | 1 | 1 | |||
| 沿A-A加載 | εA1（με） | εA2（με） | εA3（με） | ||||||||||||
| 0.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1.3 | 393 | 392 | 389 | 391.3 | 124 | 124 | 124 | 124 | -148 | -147 | -147 | -147.3 | |||
| 0.3 | 4 | -1 | 0 | 1 | 0 | -2 | 0 | -0.7 | -3 | 0 | 0 | -1 | |||
五、數據處理
1. 根據實驗數據計算出偏心拉伸時的拉應力、彎曲應力和橫截面中性軸位置。
答：根據上面實驗數據，結合材料力學相關知識計算如下：
（1）由實驗數據可知，
和
處的正應力值為：
和
處的正應力值為：
和
處的正應力值為：
通過對稱軸線加載時的平均應變為：
所以，拉應力為：
（2）由實驗數據可知，通過
截面加載時
和
處的彎曲應力為：
和
處的彎曲應力為：
和處的彎曲應力為：
（3）距離中心軸距離為y處總應力為：
所以，設中性軸距離中心軸線距離為y，則有：
其中：
所以，可以得到：
解得：
所以，橫截面中性軸位置為：距離中心軸線
處。2. 理論計算試件偏心拉伸時的拉應力、彎曲應力和橫截面中性軸位置。
答：根據材料力學知識分析如下：
（1）拉應力為：
（2）彎曲應力為：
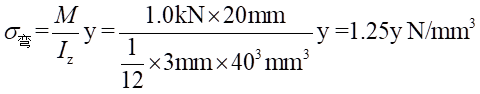
所以，距離中心軸線+15mm處的
和
處的彎曲應力為：
位于中心軸上的
和
處的彎曲應力為：
距離中心軸線-15mm處的
和
處的彎曲應力為：
（3）距離中心軸距離為y處總應力為：
所以，設中性軸距離中心軸線距離為y，則有：
即：
解得：
所以，橫截面中性軸位置為：距離中心軸線
處。4. 比較、分析實驗結果與理論計算之差異。
答：結合材料力學相關知識計算如下：
（1）拉應力比較：
理論值：
測量值：
相對誤差為：
（2）彎曲應力比較：
a.應變片R1和R2處的彎曲應力：
理論值：
測量值：
相對誤差為：
b.應變片R3和R4處的彎曲應力：
理論值：
測量值：
絕對誤差為：
c.應變片R5和R6處的彎曲應力：
理論值：
測量值：
相對誤差為：
（3）橫截面中性軸位置比較：
理論值：
測量值：
相對誤差為：
六、實驗結果
根據前面計算可以看出，實驗計算的結果和理論計算的結果基本吻合。現列表如下：
表5-2 結果對比表
| 比較對象 | 理論值 | 實驗值 | 相對誤差/% |
| 拉應力/MPa | 8.333 | 8.12 | 2.556 |
| 彎曲應力R1R2/MPa | 18.75 | 17.926 | 4.203 |
| 中性軸位置/mm | -6.665 | -6.496 | 2.536 |
七、思考題
1． 本實驗，若不采用通過試件對稱軸和通過偏心A-A截面兩次加載，是否能分離出分別由軸力引起的應力和由彎矩引起的應力？
答：能。該實驗中軸力的作用效果是改變了中性軸位置。所以要想知道軸力的大小，我們實驗研究的重點也應該是試件中性軸的變化情況。根據材料力學可以知道，所謂的中性軸也就是沒有應變的軸線。所以所以我們可以通過實驗找到中性軸的大小來反過來求軸力和彎矩引起的應力值的大小。
2． 本實驗采用串聯單臂半橋連接方式，可解決測試中出現的什么問題？
答：可以解決實驗中出現的上下表面應變不同，從而提高實驗的精度。
3． 當通過試件對稱軸加載時，3組應變片（R1和R2，R3和R4，R5和R6）讀數應變是否應該相同？
答：不相同。因為該實驗這種加載施加的是集中載荷。材料力學公式的試用性是在圣維南原理的基礎上。現實情況，截面上各個點的受力情況不盡相同，所以應變也不應該一樣。但這并不能否認材料力學的知，我們用材料力學計算的結果已經很接近真實解，并且滿足工程要求。